Chapter 3: Worksheet 1 Jack K. Cohen Colorado School of Mines
The Derivative as the Slope Function
Suggested Problems
Section 3.1: 6, 8, 14, 16
- We already have an arsenal of knowledge about slopes. Fill in the blanks with words that make the sentences correct mathematical statements. The slope of f (x) at x = a is the _______________ of the function at x = a. If f (x) is increasing on the interval
[x1, x2] then the derivative is _______________ on this interval. If the slope is negative on an interval, then the function is _______________ there. If the slope is negative on [a, c) and positive on (c, b] and the function is continuous at c, then the function has a _______________ at x = c. If the derivative is positive on [a, c) and negative on (c, b] and the function is continuous at c, then the function has a _______________ at x = c.
- Use the notions reviewed in the previous question and the fact that the derivative of
y = ax3 + bx2 + cx + d is
 = 3ax2 + 2bx + c (this is proved in section 3.2) to find the x-values that give the maximum and minimum of
f (x) = x3 - 2x + 1 on the closed interval [- 1, 1].
= 3ax2 + 2bx + c (this is proved in section 3.2) to find the x-values that give the maximum and minimum of
f (x) = x3 - 2x + 1 on the closed interval [- 1, 1].
- Same as last question, but for the closed interval [- 2, 2].
- Make a hand sketch of the slope function on [- 2, 2] for the f (x) used in the previous two problems.
- We know that the exact slope function or derivative f'(x) of a given function f (x) involves a limit process. However,
f'(x)

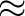 is a good approximation when h is ``small''. In this exercise, we want to investigate derivatives of functions using this insight. We will use the following code:
is a good approximation when h is ``small''. In this exercise, we want to investigate derivatives of functions using this insight. We will use the following code:
f[x_] := x^2;
h = .01;
a = -2;
b = 2;
fs[x_] := (f[x + h] - f[x])/h
Plot[{f[x], fs[x]}, {x, a, b},
PlotStyle -> {GrayLevel[0], GrayLevel[0.5]}
]
Run the above code block. Does the graph of the approximate slope function (the lighter graph) agree fairly well with the known derivative of the given function? Justify your answer using complete sentences.
- Alter the above code block to examine the function
f (x) = sin x (which is written in as f[x_] := Sin[x]) on the interval
[- π, π] (written in as {x, -Pi, Pi}). The approximate derivative function (the lighter graph) is an old friend—tell what function it is. Check up a bit on your answer by estimating an appropriate number from the graph. Conclusion: dollars to donuts the derivative of sin x is ________.
- Which is the function and which is the derivative? Prove that it could not be the other way round and that the way you pick is consistent. Note that it is not sufficient to just say something like ``when f' is positive, f is increasing'' since this is always true. You have to pin such assertions to specific intervals relevant to the given function.
- See Figure 1.
Figure:
Which is the derivative?
 |
- See Figure 2.
Figure:
Which is the derivative?
 |
- See Figure 3.
Figure:
Which is the derivative?
 |
 = 3ax2 + 2bx + c (this is proved in section 3.2) to find the x-values that give the maximum and minimum of
f (x) = x3 - 2x + 1 on the closed interval [- 1, 1].
= 3ax2 + 2bx + c (this is proved in section 3.2) to find the x-values that give the maximum and minimum of
f (x) = x3 - 2x + 1 on the closed interval [- 1, 1].

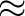 is a good approximation when h is ``small''. In this exercise, we want to investigate derivatives of functions using this insight. We will use the following code:
is a good approximation when h is ``small''. In this exercise, we want to investigate derivatives of functions using this insight. We will use the following code:


